SV39多级页表机制：内容介绍¶

本节导读¶

在上一小节中我们已经简单介绍了分页的内存管理策略，现在我们尝试在 RV64 架构提供的 SV39 分页机制的基础上完成内核中的软件对应实现。由于内容过多，我们将分成两个小节进行讲解。本节主要讲解在RV64架构下的虚拟地址与物理地址的访问属性（可读，可写，可执行等），组成结构（页号，帧号，偏移量等），访问的空间范围等；以及我们在OS中如何进行页表的处理。

虚拟地址和物理地址¶

内存控制相关的CSR寄存器¶

默认情况下 MMU 未被使能，此时无论 CPU 位于哪个特权级，访存的地址都会作为一个物理地址交给对应的内存控制单元来直接访问物理内存。我们可以通过修改 S 特权级的一个名为 satp 的 CSR 来启用分页模式，在这之后 S 和 U 特权级的访存地址会被视为一个虚拟地址，它需要经过 MMU 的地址转换变为一个物理地址，再通过它来访问物理内存；而 M 特权级的访存地址，我们可设定是内存的物理地址。

注解

M 特权级的访存地址被视为一个物理地址还是一个需要经历和 S/U 特权级相同的地址转换的虚拟地址取决于硬件配置，在这里我们不会进一步探讨。

上图是 RV64 架构下 satp 的字段分布。当 MODE 设置为 0 的时候，代表所有访存都被视为物理地址；而设置为 8 的时候，SV39 分页机制被启用，所有 S/U 特权级的访存被视为一个 39 位的虚拟地址，它们需要先经过 MMU 的地址转换流程，如果顺利的话，则会变成一个 56 位的物理地址来访问物理内存；否则则会触发异常，这体现了该机制的内存保护能力。

虚拟地址和物理地址都是字节地址，39 位的虚拟地址可以用来访问理论上最大 \(512\text{GiB}\) 的地址空间，而 56 位的物理地址在理论上甚至可以访问一块大小比这个地址空间的还高出几个数量级的物理内存。但是实际上无论是虚拟地址还是物理地址，真正有意义、能够通过 MMU 的地址转换或是 CPU 内存控制单元的检查的地址仅占其中的很小一部分，因此它们的理论容量上限在目前都没有实际意义。

地址格式与组成¶

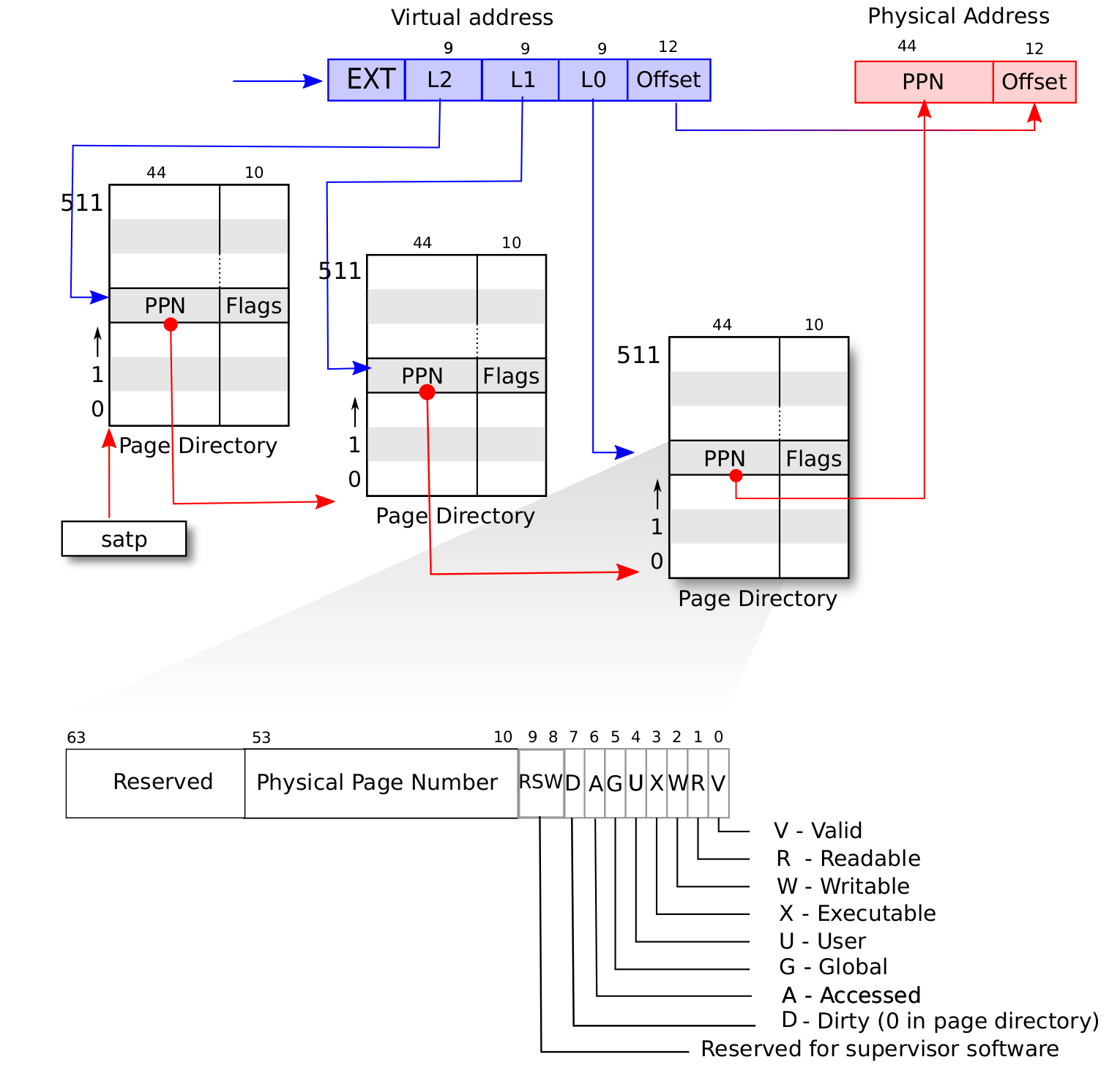
我们采用分页管理，单个页面的大小设置为 \(4\text{KiB}\) ，每个虚拟页面和物理页帧都对齐到这个页面大小，也就是说虚拟/物理地址区间 \([0,4\text{KiB})\) 为第 \(0\) 个虚拟页面/物理页帧，而 \([4\text{KiB},8\text{KiB})\) 为第 \(1\) 个，以此类推。 \(4\text{KiB}\) 需要用 12 位字节地址来表示，因此虚拟地址和物理地址都被分成两部分：它们的低 12 位，即 \([11:0]\) 被称为 页内偏移 (Page Offset) ，它描述一个地址指向的字节在它所在页面中的相对位置。而虚拟地址的高 27 位，即 \([38:12]\) 为它的虚拟页号 VPN，同理物理地址的高 44 位，即 \([55:12]\) 为它的物理页号 PPN，页号可以用来定位一个虚拟/物理地址属于哪一个虚拟页面/物理页帧。

地址转换是以页为单位进行的，在地址转换的前后地址的页内偏移部分不变。可以认为 MMU 只是从虚拟地址中取出 27 位虚拟页号，在页表中查到其对应的物理页号（如果存在的话），最后将得到的44位的物理页号与虚拟地址的12位页内偏移依序拼接到一起就变成了56位的物理地址。

注解

RV64 架构中虚拟地址为何只有 39 位？

在 64 位架构上虚拟地址长度确实应该和位宽一致为 64 位，但是在启用 SV39 分页模式下，只有低 39 位是真正有意义的。 SV39 分页模式规定 64 位虚拟地址的 \([63:39]\) 这 25 位必须和第 38 位相同，否则 MMU 会直接认定它是一个不合法的虚拟地址。通过这个检查之后 MMU 再取出低 39 位尝试将其转化为一个 56 位的物理地址。

也就是说，所有 \(2^{64}\) 个虚拟地址中，只有最低的 \(256\text{GiB}\) （当第 38 位为 0 时）以及最高的 \(256\text{GiB}\) （当第 38 位为 1 时）是可能通过 MMU 检查的。当我们写软件代码的时候，一个地址的位宽毋庸置疑就是 64 位，我们要清楚可用的只有最高和最低这两部分，尽管它们已经巨大的超乎想象了；而本节中我们专注于介绍 MMU 的机制，强调 MMU 看到的真正用来地址转换的虚拟地址只有 39 位。

多级页表原理¶

页表的一种最简单的实现是线性表，也就是按照地址从低到高、输入的虚拟页号从 \(0\) 开始递增的顺序依次在内存中（我们之前提到过页表的容量过大无法保存在 CPU 中）放置每个虚拟页号对应的页表项。由于每个页表项的大小是 \(8\) 字节，我们只要知道第一个页表项（对应虚拟页号 \(0\) ）被放在的物理地址 \(\text{base_addr}\) ，就能直接计算出每个输入的虚拟页号对应的页表项所在的位置。如下图所示：

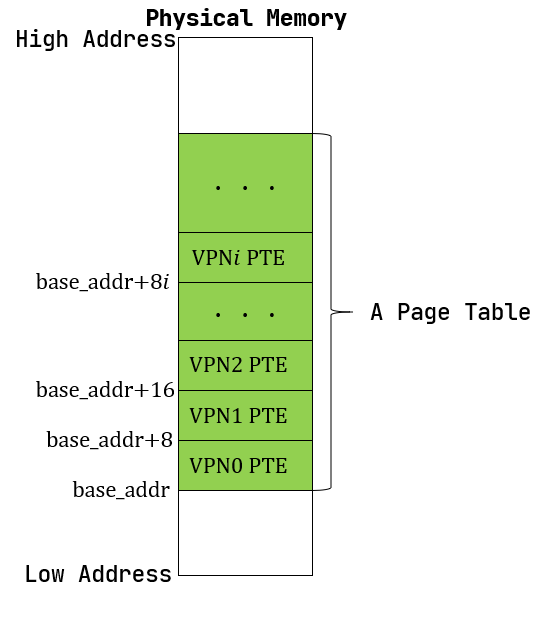
事实上，对于虚拟页号 \(i\) ，如果页表（每个应用都有一个页表，这里指其中某一个）的起始地址为 \(\text{base_addr}\) ，则这个虚拟页号对应的页表项可以在物理地址 \(\text{base_addr}+8i\) 处找到。这使得 MMU 的实现和内核的软件控制都变得非常简单。然而遗憾的是，这远远超出了我们的物理内存限制。由于虚拟页号有 \(2^{27}\) 种，每个虚拟页号对应一个 \(8\) 字节的页表项，则每个页表都需要消耗掉 \(1\text{GiB}\) 内存！应用的数据还需要保存在内存的其他位置，这就使得每个应用要吃掉 \(1\text{GiB}\) 以上的内存。作为对比，我们的 K210 开发板目前只有 \(8\text{MiB}\) 的内存，因此从空间占用角度来说，这种线性表实现是完全不可行的。

线性表的问题在于：它保存了所有虚拟页号对应的页表项，但是高达 \(512\text{GiB}\) 的地址空间中真正会被应用使用到的只是其中极小的一个子集（本教程中的应用内存使用量约在数十~数百 \(\text{KiB}\) 量级），也就导致有意义并能在页表中查到实际的物理页号的虚拟页号在 \(2^{27}\) 中也只是很小的一部分。由此线性表的绝大部分空间其实都是被浪费掉的。

那么如何进行优化呢？核心思想就在于 按需分配 ，也就是说：有多少合法的虚拟页号，我们就维护一个多大的映射，并为此使用多大的内存用来保存映射。这是因为，每个应用的地址空间最开始都是空的，或者说所有的虚拟页号均不合法，那么这样的页表自然不需要占用任何内存， MMU 在地址转换的时候无需关心页表的内容而是将所有的虚拟页号均判为不合法即可。而在后面，内核已经决定好了一个应用的各逻辑段存放位置之后，它就需要负责从零开始以虚拟页面为单位来让该应用的地址空间的某些部分变得合法，反映在该应用的页表上也就是一对对映射顺次被插入进来，自然页表所占据的内存大小也就逐渐增加。

这种思想在计算机科学中得到了广泛应用：为了方便接下来的说明，我们可以举一道数据结构的题目作为例子。设想我们要维护一个字符串的多重集，集合中所有的字符串的字符集均为 \(\alpha=\{a,b,c\}\) ，长度均为一个给定的常数 \(n\) 。该字符串集合一开始为空集。我们要支持两种操作，第一种是将一个字符串插入集合，第二种是查询一个字符串在当前的集合中出现了多少次。

简单起见，假设 \(n=3\) 。那么我们可能会建立这样一颗 字典树 (Trie) ：

字典树由若干个节点（图中用椭圆形来表示）组成，从逻辑上而言每个节点代表一个可能的字符串前缀。每个节点的存储内容都只有三个指针，对于蓝色的非叶节点来说，它的三个指针各自指向一个子节点；而对于绿色的叶子节点来说，它的三个指针不再指向任何节点，而是具体保存一种可能的长度为 \(n\) 的字符串的计数。这样，对于题目要求的两种操作，我们只需根据输入的字符串中的每个字符在字典树上自上而下对应走出一步，最终就能够找到字典树中维护的它的计数。之后我们可以将其直接返回或者加一。

注意到如果某些字符串自始至终没有被插入，那么一些节点没有存在的必要。反过来说一些节点是由于我们插入了一个以它对应的字符串为前缀的字符串才被分配出来的。如下图所示：

一开始仅存在一个根节点。在我们插入字符串 acb 的过程中，我们只需要分配 a 和 ac 两个节点。注意 ac 是一个叶节点，它的 b 指针不再指向另外一个节点而是保存字符串 acb 的计数。此时我们无法访问到其他未分配的节点，如根节点的 b/c 或是 a 节点的 a/b 均为空指针。如果后续再插入一个字符串，那么 至多分配两个新节点 ，因为如果走的路径上有节点已经存在，就无需重复分配了。这可以说明，字典树中节点的数目（或者说字典树消耗的内存）是随着插入字符串的数目逐渐线性增加的。

读者可能很好奇，为何在这里要用相当一部分篇幅来介绍字典树呢？事实上 SV39 分页机制等价于一颗字典树。 \(27\) 位的虚拟页号可以看成一个长度 \(n=3\) 的字符串，字符集为 \(\alpha=\{0,1,2,...,511\}\) ，因为每一位字符都由 \(9\) 个比特组成。而我们也不再维护所谓字符串的计数，而是要找到字符串（虚拟页号）对应的页表项。因此，每个叶节点都需要保存 \(512\) 个 \(8\) 字节的页表项，一共正好 \(4\text{KiB}\) ，可以直接放在一个物理页帧内。而对于非叶节点来说，从功能上它只需要保存 \(512\) 个指向下级节点的指针即可，不过我们就像叶节点那样也保存 \(512\) 个页表项，这样所有的节点都可以被放在一个物理页帧内，它们的位置可以用一个物理页号来代替。当想从一个非叶节点向下走时，只需找到当前字符对应的页表项的物理页号字段，它就指向了下一级节点的位置，这样非叶节点中转的功能也就实现了。每个节点的内部是一个线性表，也就是将这个节点起始物理地址加上字符对应的偏移量就找到了指向下一级节点的页表项（对于非叶节点）或是能够直接用来地址转换的页表项（对于叶节点）。

这种页表实现被称为 多级页表 (Multi-Level Page-Table) 。由于 SV39 中虚拟页号被分为三级 页索引 (Page Index) ，因此这是一种三级页表。

非叶节点的页表项标志位含义和叶节点相比有一些不同：

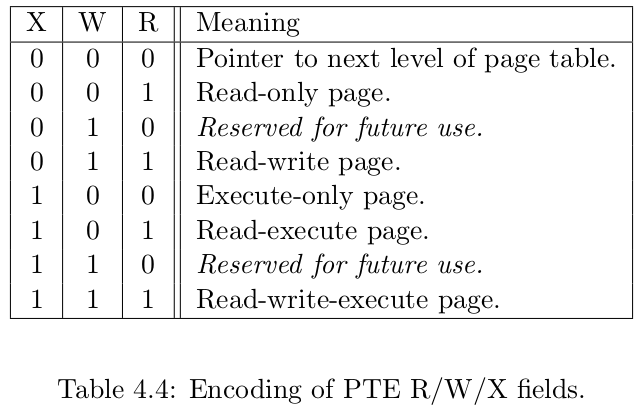
当 V 为 0 的时候，代表当前指针是一个空指针，无法走向下一级节点，即该页表项对应的虚拟地址范围是无效的；
只有当V 为1 且 R/W/X 均为 0 时，表示是一个合法的页目录表项，其包含的指针会指向下一级的页表。
注意: 当V 为1 且 R/W/X 不全为 0 时，表示是一个合法的页表项，其包含了虚地址对应的物理页号。

在这里我们给出 SV39 中的 R/W/X 组合的含义：

注解

大页 (Huge Page)

本教程中并没有用到大页的知识，这里只是作为拓展，不感兴趣的读者可以跳过。

事实上正确的说法应该是：只要 R/W/X 不全为 0 就会停下来，直接从当前的页表项中取出物理页号进行最终的地址转换。如果这一过程并没有发生在多级页表的最深层，那么在地址转换的时候并不是直接将物理页号和虚拟地址中的页内偏移接在一起得到物理地址，这样做会有问题：由于有若干级页索引并没有被使用到，即使两个虚拟地址的这些级页索引不同，还是会最终得到一个相同的物理地址，导致冲突。

我们需要重新理解将物理页号和页内偏移“接起来”这一行为，它的本质是将物理页号对应的物理页帧的起始物理地址和页内偏移进行求和，前者是将物理页号左移上页内偏移的位数得到，因此看上去恰好就是将物理页号和页内偏移接在一起。但是如果在从多级页表往下走的中途停止，未用到的页索引会和虚拟地址的 \(12\) 位页内偏移一起形成一个位数更多的页内偏移，也就对应于一个大页，在转换物理地址的时候，其算法仍是上述二者求和，但那时便不再是简单的拼接操作。

在 SV39 中，如果使用了一级页索引就停下来，则它可以涵盖虚拟页号的前 \(9\) 位为某一固定值的所有虚拟地址，对应于一个 \(1\text{GiB}\) 的大页；如果使用了二级页索引就停下来，则它可以涵盖虚拟页号的前 \(18\) 位为某一固定值的所有虚拟地址，对应于一个 \(2\text{MiB}\) 的大页。以同样的视角，如果使用了所有三级页索引才停下来，它可以涵盖虚拟页号为某一个固定值的所有虚拟地址，自然也就对应于一个大小为 \(4\text{KiB}\) 的虚拟页面。

使用大页的优点在于，当地址空间的大块连续区域的访问权限均相同的时候，可以直接映射一个大页，从时间上避免了大量页表项的索引和修改，从空间上降低了所需节点的数目。但是，从内存分配算法的角度，这需要内核支持从物理内存上分配三种不同大小的连续区域（ \(4\text{KiB}\) 或是另外两种大页），便不能使用更为简单的插槽式管理。权衡利弊之后，本书全程只会以 \(4\text{KiB}\) 为单位进行页表映射而不会使用大页特性。

那么 SV39 多级页表相比线性表到底能节省多少内存呢？这里直接给出结论：设某个应用地址空间实际用到的区域总大小为 \(S\) 字节，则地址空间对应的多级页表消耗内存为 \(\frac{S}{512}\) 左右。下面给出了详细分析，对此不感兴趣的读者可以直接跳过。

注解

分析 SV39 多级页表的内存占用

我们知道，多级页表的总内存消耗取决于节点的数目，每个节点则需要一个大小为 \(4\text{KiB}\) 物理页帧存放。不妨设某个应用地址空间中的实际用到的总空间大小为 \(S\) 字节，则多级页表所需的内存至少有这样两个上界：

每映射一个 \(4\text{KiB}\) 的虚拟页面，最多需要新分配两个物理页帧来保存新的节点，加上初始就有一个根节点，因此消耗内存不超过 \(4\text{KiB}\times(1+2\frac{S}{4\text{KiB}})=4\text{KiB}+2S\) ；
考虑已经映射了很多虚拟页面，使得根节点的 \(512\) 个孩子节点都已经被分配的情况，此时最坏的情况是每次映射都需要分配一个不同的最深层节点，加上根节点的所有孩子节点并不一定都被分配，从这个角度来讲消耗内存不超过 \(4\text{KiB}\times(1+512+\frac{S}{4\text{KiB}})=4\text{KiB}+2\text{MiB}+S\) 。

虽然这两个上限都可以通过刻意构造一种地址空间的使用来达到，但是它们看起来很不合理，因为它们均大于 \(S\) ，也就是元数据比数据还大。其实，真实环境中一般不会有如此极端的使用方式，更加贴近实际的是下面一种上限：即除了根节点的一个物理页帧之外，地址空间中的每个实际用到的大小为 \(T\) 字节的连续区间会让多级页表额外消耗不超过 \(4\text{KiB}\times(\lceil\frac{T}{2\text{MiB}}\rceil+\lceil\frac{T}{1\text{GiB}}\rceil)\) 的内存。这是因为，括号中的两项分别对应为了映射这段连续区间所需要新分配的最深层和次深层节点的数目，前者每连续映射 \(2\text{MiB}\) 才会新分配一个，而后者每连续映射 \(1\text{GiB}\) 才会新分配一个。由于后者远小于前者，可以将后者忽略，最后得到的结果近似于 \(\frac{T}{512}\) 。而一般情况下我们对于地址空间的使用方法都是在其中放置少数几个连续的逻辑段，因此当一个地址空间实际使用的区域大小总和为 \(S\) 字节的时候，我们可以认为为此多级页表消耗的内存在 \(\frac{S}{512}\) 左右。相比线性表固定消耗 \(1\text{GiB}\) 的内存，这已经相当可以接受了。

上面主要是对一个固定应用的多级页表进行了介绍。在一个多任务系统中，可能同时存在多个任务处于运行/就绪状态，它们的多级页表在内存中共存，那么 MMU 应该如何知道当前做地址转换的时候要查哪一个页表呢？回到 satp CSR 的布局，其中的 PPN 字段指的就是多级页表根节点所在的物理页号。因此，每个应用的地址空间就可以用包含了它多级页表根节点所在物理页号的 satp CSR 代表。在我们切换任务的时候， satp 也必须被同时切换。

最后的最后，我们给出 SV39 地址转换的全过程图示来结束多级页表原理的介绍：